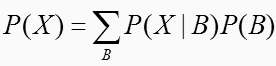 |
私の研究領域は、「画像処理における逆問題」という、今にして思えば手がけるんじゃなかったと後悔するような厄介なシロモノです。
以前読んだ論文の中で、減色した画像のカラーパレットを復元するという研究に、「最尤推定・ベイズ推定」というキーワードがありました。これは武器になるのか否か。一縷の望みを託して、専門書と向き合ってみました。
ですから、これは「私のノート」です。解説書ではないことをご承知願います。
客観確率に加えて主観確率をも含めた広義の確率をベイズ確率と呼ぶ。
客観確率を基礎とする確率論は、ベイズ確率においても同様に適用できることが証明されている。例えばコインにおいて、それぞれの面が出る確率が等しく1/2であるということは、
ある証拠に基づいて、その原因となった事象を推定するための確率論的方法。後述の「ベイズの定理」を用いて、新しい証拠に照らして命題の尤もらしさを改訂していく方法である。この方法は人間の思考様式を反映しているといえる。
観測しうる事象。ここでAは離散確率変数である。
観測者は、ある観測対象に対して、Aという事象があることを認識しているとする。その事象が起こる確率をP(A)とする。P(A)は、事前確率と呼ばれ、観測者が観測以前に持っている信念を確率分布関数で表現している。
通常、事前確率は、想定される原因事象の総和が100%となるように設定される。
観測において、実際に確認した事象。または事象を判別するための条件。ここで X は離散確率変数である
ベイズ推定では、事前に認識した確率変数A に対する信念は、X の確認をきっかけに変化すると考える。
観測者が、X を確認したとする。このとき、X
のもとで事象 A が起こる確率を P(A|X)
として改訂する。P(A|X)は、事後確率と呼ばれ、世界を
X に限定したときに事象 A
が発生する条件付き確率を確率分布関数で表現している。
通常、事後確率は、想定される原因事象の総和が100%となるように設定される。
観測者の経験から、観測結果 P(X) は、かつて事象 A
が原因で起こったという傾向を正しく認識しているとする。このとき
X は、確率 P(X|A)
に従って生成されるはずである。 P(X|A) を X
が観測されたときの X の尤度(ゆうど)と呼ぶ。または、これを尤度関数(likelihood
function) L(A|X) = P(X|A)
で定義された確率的生成モデルと呼ぶこともある。ここで、L(A|X)は
A に関する確率分布を示すものではない。A
は、その値によって X の生起が変るという意味で、 A
を P(X|A) のパラメータと呼ぶこともある。
通常、尤度は、想定される原因事象に対して、想定される結果の総和が100%となるように設定される。
コインを投げるとき、二回続けて同じ結果が得られた場合を考えると、
観測結果であり、判断材料 X のそれぞれを確認した割合を、確率として示したもの。以下の式で示される。
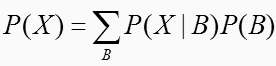 |
ここで、 B は、 A について想定されるすべての原因事象を示す。
P(A)、P(A|X)、P(X|A)の間には、以下の式で示される関係が成り立つ。これをベイズの定理という。
ベイズ確率の考え方では、A
を定数とする必要はなく、ある分布に従う確率変数としてよい。
事象 X が発生した下では P(X)
は定数となることから、ベイズの定理の式は、データを得た下で、主観確率分布に既知の尤度を加味することによって、より客観性の高い確率分布へと更新する関係を示している。この確率分布の更新をベイズ改訂と呼ぶ。
いくつかの仮説を比較するとき、客観確率では、仮説に基づいて実際の観測値が得られる確率をもって仮説の採択か棄却かを行う。一方ベイズ確率では、ある仮説がもう1つの仮説よりも確からしい、あるいは一方の仮説を採択する際に期待される損失がもう一方を採択する際の損失より小さい、といった観点で比較がなされる。
状況 A のもとで行動 D を決定するとき、行動 D の良さは、効用関数(utility function) U(D|A) で定義されるものとする。不確実な状況 A のもとでの最良の行動は、期待効用 E[U] が最大になるように定められる。 E[U] は以下の式で表される。
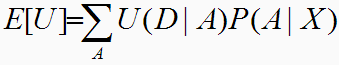 |
事後確率のもとで、ある行動において、何らかのリスク(メリット)を受けるとき、それに伴うコスト(効用)が発生する場合、コストを数値化したものが U(D|A) にあたる。
事前に構造が明らかでなく、多くの試行が困難であるとき、主観的な確率を求める計算方法として、ベイズ推定は実用性がある。
系統推定における最尤法は頻度主義であり、尤度を目的関数として、それを最大化する樹形を探索する。一方、ベイズ推定はベイズ主義を背景とし、事後確率を目的関数として、それを最大化する樹形を求める。ベイズの定理から、尤度の大小は必ずしも事後確率の大小とは相関しない。尤度が大きくても事前確率が小さければ、事後確率はそれに比例して小さくなるためである。
ベイズ推定では、事前確率をどのように設定するかが問題となる。通常は、そのカテゴリに含まれる標本の割合で推定されるが、データがなければ系統樹の生じる確率は不明であり、事前確率には等確率を置くことになる。この場合、
| P[A | X] = P[X | A] ・ P[A] / P[X] |
の P[A] / P[X] は定数となるため、最尤法とベイズ推定の結果は必ず等しくなる。
事前確率の問題に加えて、ベイズ推定には、計算量の負担が大きいという実際的な問題もある。特にP(X)の計算は、膨大な系統に対する総和を必要とし、尤度計算にはパラメーターごとの数値積分が要求される。当然、解析的に事後確率を計算することは不可能である。この問題を現実のデータから解決する手法が1990年代半ばに開発された「経験ベイズ法(EB)」と「マルコフ連鎖モンテカルロ法(MCMC)」である。これらの方法は、ベイズ推定の問題であった事前確率をデータから推定する方策(EB)を与え、大量の計算をマルコフ連鎖に基づく数値最適化の手法(MCMC)を適用するということで、現実のデータに基づく事後確率の計算を可能にしている。
経験ベイズ法では、事前確率を制御する目的でパラメータを用意する。本質としては、客観的な方法で事前確率を設定しなければ意味のある推定結果が得られないためである。このパラーメータをハイパーパラメータと呼ぶ。ハイパーパラメータは主観的に決めることもできるが、経験ベイズ法では、データからハイパーパラメータを推定する。具体的にはハイパーパラメータについても事前確率を仮定して事前確率を拡張することによって、事後確率を階層的に表現する。ここでハイパーパラメータに一様分布を仮定すると、ハイパーパラメータは、その周辺分布(周辺尤度)を最大化するように定められる。
MCMC法とは、ある分布からサンプリングを行う際に、 1回前にサンプリングされた値に依存させて次のサンプリングを行う方法の総称である。ある分布から乱数を生成して統計量を推定するのがモンテカルロ積分である。目的の分布からの乱数発生を直接行うことが難しい場合に、Markov連鎖を使って、定常分布が目的の分布になるような乱数を作るのが
MCMC である。MCMCでは、初期系統樹の樹形を撹乱することによって、より事後確率の高い系統樹を発見的に探索していく。この探索過程(定常マルコフ連鎖)を繰り返すことによって次第に収束していくならば、最終的に事後確率分布が得られることとなる。
代表的な手法にGibbs SamplerとMetropolis-Hastingsアルゴリズムがある。この方法を使うと、最小2乗法や最尤法で推定できないようなモデルでもベイズ推定することが可能になる。
2008/05/24: 作成